Topology: Sequentially Compact Spaces and Compact Spaces | Mathematics and Such
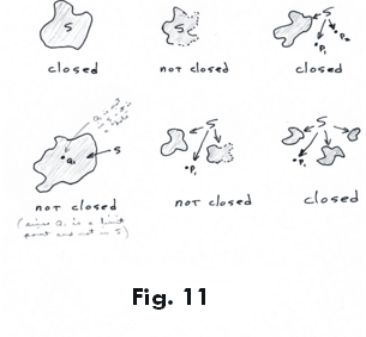
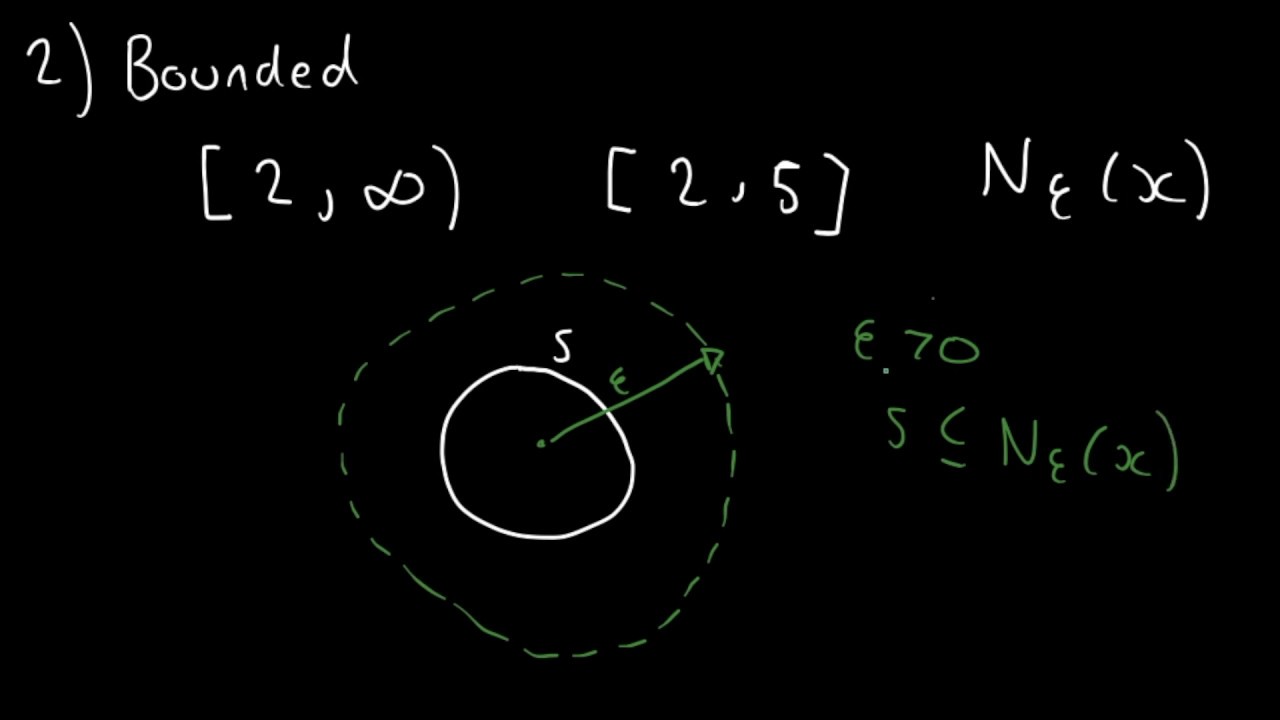SOLVED: Set is closed (a bounded set). Which of the following sets in R' is compact? a. x,y,z: 2 < x+y+2 < 4 b. x,y,2:k+y+d<s c. x,y,z: -1 < x < y <
Answered: Let (X, d) be a metric space. In this… | bartleby
Understanding Compact Sets - YouTube
Bounded set - Wikipedia
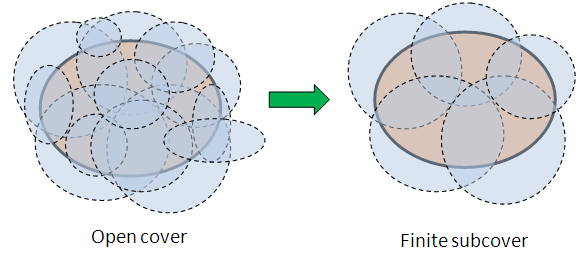
Fractals. Compact Set Compact space X E N A collection {U ; U E N } of open sets, X U .A collection {U ; U E N } of open sets, X. - ppt download
Compact space - Wikipedia
Metric Spaces. Chapter 1 - PDF Free Download
Compact, Open, Closed and Bounded Sets
Continuous Functions on Compact Sets of Metric Spaces - Mathonline
SOLVED: In the lecture, we proved that a set E ∈ ℠^n is compact if and only if it is closed and bounded. In this problem, we will explore whether this
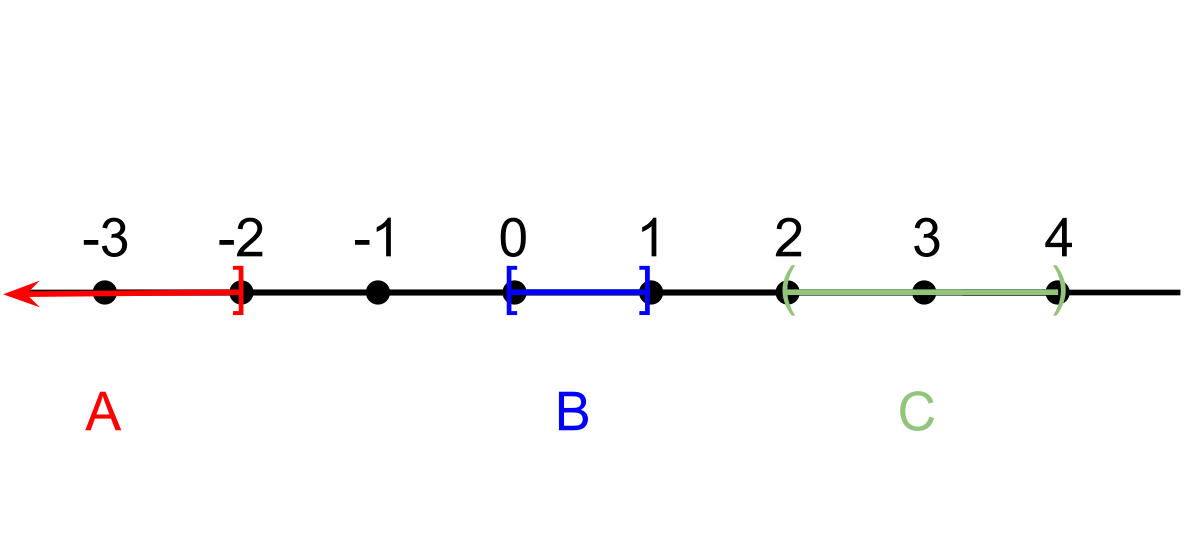
general topology - Determining if following sets are closed, open, or compact - Mathematics Stack Exchange
6. use the definition of a compact set to prove that the union of two compact sets
Decide whether the following propositions are true or false. | Quizlet
PDF) On Sequential Compactness and Related Notions of Compactness of Metric Spaces in $\mathbf {ZF}
Analysis WebNotes: Chapter 06, Class 31
Solved Exercise 8 please . Chapter is about complete & | Chegg.com
Analysis WebNotes: Chapter 06, Class 31
Define a compact set. use your definition to prove thatt (i) the set r is not compact;
Compact Sets are Closed and Bounded - YouTube
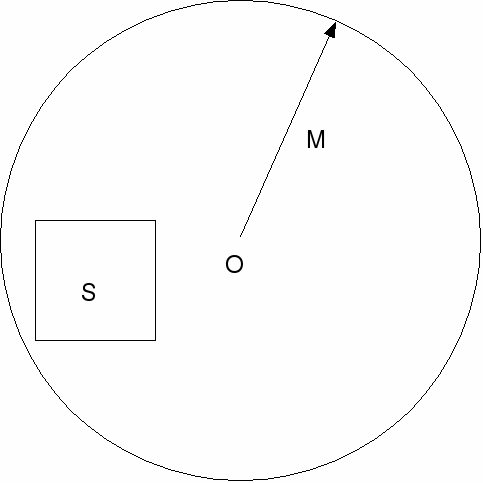
general topology - Visual representation of difference between closed, bounded and compact sets - Mathematics Stack Exchange
Math 512A. Homework 6 Solutions
Solved Problem 4. Let (X,d) be a totally bounded metric | Chegg.com
Compact Set, Proper Spaces and Annulus - Cheenta
The Extreme Value Theorem for Cts. Fns. on Comp. Sets of Met. Sps. - Mathonline
Point sets in one, two, three and n-dimensional Euclidean spaces. Neighborhoods, closed sets, open sets, limit points, isolated points. Interior, exterior and boundary points. Derived set. Closure of a set. Perfect set.
